Algoritmy zpracování textů – operace s řetězci, porovnání se vzorem (KMP, Boyer-Moore algoritmus), nejdelší společný podřetězec (LCS algoritmus), vzdálenost mezi řetězci, datová struktura Trie a použití
Tak tahle otázka je očistec. Kdo tohle všechno vysvětlí za 15 minut je borec, i když bych řekl, že je tam rozsekaj na menší otázky.
Obsah |
Obecně
Vyhledáváme podřetězec P v řetězci T. T je string s textem, P je string s maskou (pattern)
Podřetězec je část řetězce [i..j]. T je délky n, P je délky m.
Prefix je část řetězce (či podřetězce) od začátku, suffix je část řetězce (či podřetězce) od konce.
Brutální síla
Indexem jdeme po T a kontrolujeme, jestli podřetězec začínající na tomto indexu neodpovídá P (tedy kontrolujeme m prvků od indexu směrem do prava. V nejhorším případě O(nm), což je pomalé
T: aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaah
P: aah
P v T najdeme až úplně na konci, pro každé 'a' v T (kromě třetího od konce) znovu hledáme písmena P v řetězci T zcela zbytečně
Boyer-Moore (BM) algoritmus
V tomto algoritmu prohledáváme P od konce, a hledáme výskyt v T. Do T ukazuje index i, do P index j.
Mohou nastat 4 případy:
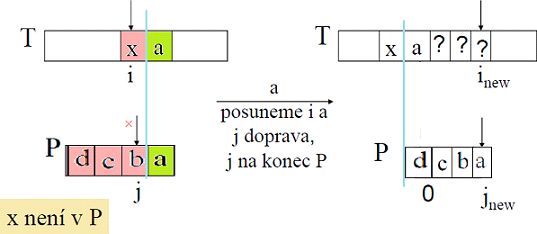
1) T[i] není v P vůbec, posuneme i dále o délku P (zarovnáme P na další písmeno v T, tedy T[i+1]
(obrázky v přednáškách jsou křivé, tak se mi to snad povedlo odstranit)
2) T[i] odpovídá P[j] - posuneme se v obou do leva a opakujeme (jako v brutální síle)
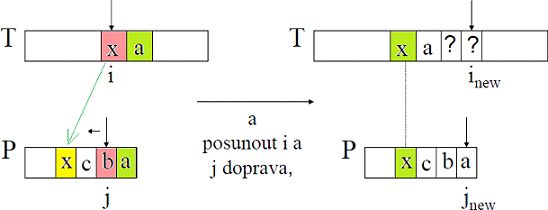
3) T[i] není P[j], ale T[i] je v P před indexem j -> zarovnáme P do prava tak, aby T[i] odpovídal jeho výskytu v P a opakujeme
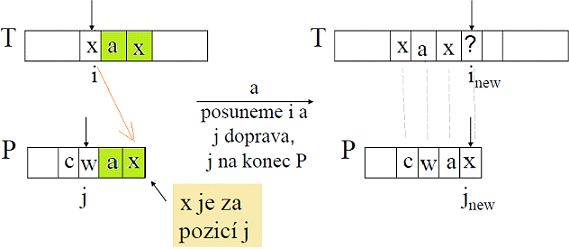
4) T[i] není P[j], ale T[i] je v P za indexem j -> posuneme se do prava o 1 a opakujeme (nemůžeme se vracet, ale ani posunout o více dále)
Pokud nalezneme celý pattern, vrátíme i. Algoritmus je pro texty rychlejší, než brute force, i tak je však jeho složitost O(mn + A), kde A je velikost abecedy. Pro velké abecedy funguje rychle, ale např pro binární soubory funguje pomalu.
Dodatek: Algoritmus si v preprocesingu zjistí, na které pozici má které písmena (směrem od leva). Je-li patern tedy například "ABRAKADABRA", A dostane index 10, B dostane index 8, K = 4, D = 6 a R = 9. Pro ostatní písmena přiřadíme -1. Naimplementujeme tedy funkci Last(char input), která podle písmene vrátí tento index, a pak pro případy 3 a 4 porovnáváme Last(T[i]) a j, a tím pak víme, jestli i posunout na Last(T[i]) (pokud je Last(T[i]) < j) nebo pouze i++
Knuth‐Morris‐Pratt (KMP) algoritmus
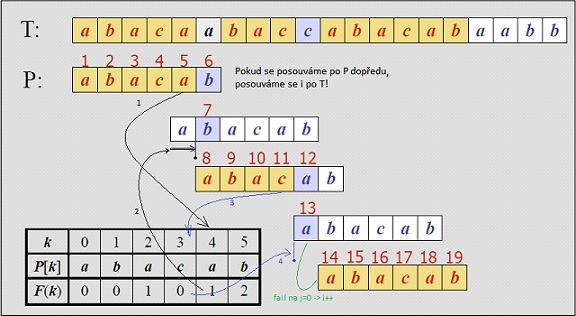
Jako brutal force jde zleva do prava, ale nedělá otrocky všechny porovnání. Pokud narazíme na neshodu, je možné se posunout o více než o jedno písmeno.
Otázka zní o kolik?
Odpověď, o maximální prefix P( 0 .. j-1 ), který je suffixem P( 1 .. j-1 ). Suffix a prefix se nesmí překrývat.
Proč? Protože najdeme-li kus P (od začátku, tedy prefix), víme, že znaky tohoto prefixu odpovídají textu. Je tedy netřeba je kontrolovat znovu. Může se ale stát, že konec nalezeného podřetězce je také obsažen v začátku tohoto podřetězce. Takovou shodou je samozřejmě celá nalezená část P, proto hledáme od P+1. Takže jdeme od konce nalezeného kusu P zleva a zprava, a ve chvíli, kdy nenalezneme shodu, víme, o kolik se můžeme posunout. Tohle se samozřejmě dá předpočítat do tabulky, a pak je vše O(1)
(i.e. P[j] != T[i]), pak k = j‐1; j = F(k); // získání nové hodnoty j, kde F(k) je právě předpočítaná tabulka společných částí P
Trie
Trie je struktura pro předspracování textu pro pozdější rychlé vyhledávání. V každém uzlu standartní Trie je písmeno a délka cesty k vrcholu je také pozicí písmene ve slově, tedy je-li hloubka písmene 'E' v Trie rovna 3, víme, že je to třetí písmeno (např. slova Trie)
Standartní trie má v každém uzlu právě jedno písmeno. Vyhledávání je O(d * m) kde d je velikost abecedy (v každém uzlu musíme projít všechna písmena, abychom zjistili, že tam písmeno je), m je délka slova. Paměťově je Trie nejvýše složitosti O(n) kde n je délka původního textu. Pokud se slova překrývají, paměťi je potřeba méně.
Rychlost se dá na úkor paměti vylepšit tak, že v každém uzlu připravíme celou abecedu a při hledání převedeme písmeno na index v této abecedě, tím pádem záskáme v O(1) čase pointer na další písmeno ve slově.
Komprimovaná trie
Jako trie, ale shlukujeme písmena. Tedy ve vrcholech stromu jsou všechna písmena, která jsou společná pro všechna slova. Tedy pro slova 'ahoj' a 'ahojky' bude mít trie 2 vrcholy, 'ahoj' a pod ním 'ahojky'. Tuto Trie lze převést na standardní pouhým rozdělením shluků, standardní Trie převedeme na kompaktní sloučením vrcholů s rodiči, kteří mají pouze jeden odkaz na vrchol (tento vrchol).
Pak je ještě suffixová Trie, která ukládá všechny sufixy slov v komprimované podobě. Umožňuje vyhledávat i uprostřed slova.
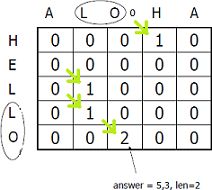
LCS - Longest common subsequence
Tohle je skoro nemožný vysvetlit na statickym papiru....
Cílem algoritmu je najít nejdelší společný podřetězec libovolného počtu řetězců. To je problém NP-těžký, což je masakr. My se ale omezíme na porovnávání 2 řezězců, což je v polynomiálním čase řešitelné (dynamicky).
Brutální síla by dělala to, že by našla všechny podřetězce obou řetězců, a ty porovnávala (také brutální silou) Podřetězců je však řekněme n!, brutální síla je n2, takže (n!)2. Dynamicky to lze dělat rychleji. Použijeme tedy rovnou dynamické programování, protože to nám dovoluje pamatovat si so už jsme našli, a neztrácet čas znovuobjevováním nalezeného.
Nechť Li,j = maximální délka společných řetězců končících v Ai a Bj . Vytvoříme si tedy dvojrozměrnou tabulku, do které si tyto Li,j budeme zapisovat.
Nyní, je-li písmeno na pozici i v řetězci A stejné, jako písmeno na pozici j v řetezci B, víme, že jde o společný podřetězec (délky 1). Nevíme však, zda předchozí písmena nebyla také podřetězcem (zatím)
Víme ale následující: Pokud existoval pořetezec pro indexy i-1 a j-1 (tedy pro předchozí písmena v obou řetězcích), bude v tabulce na příslušné pozici, tedy vlevo nahoře od Li,j tedy Li-1,j-1. Na této pozici je tím pádem dosavadně nalezená délka společného podřetězce, který končí na indexech i-1 a j-1. Pokud by i předchozí indexy daly stejné písmeno, musíme tuto délku dále diagonálně propagovat, a tedy
Ai = Bj -> Li,j = Li-1,j-1 + 1 -> společný řetězec končící na indexu i-1,j-1 pokračuje
Ai <> Bj -> Li,j = 0 -> není společný (pokud na i-1 a j-1 byl, na tomto indexu končí)
Takto vyplníme celou tabulku, přičemž nulté řádky budou nulové (abychom nevyšli pro první písmena z hranice pole)
Problém: Jak zjistit, kde je řešení nejlepší? Ano, můžeme najít maximum v tabulce, ale to je další O(M + N) operace, a máme tabulku plnou nul, toho lze využít. Algoritmus tedy modifikujeme tak, že bude zachovávat i dosavadně nejlepší nalezenou délku společného podřetězce v každém bodě. toho docílíme úpravou druhého pravidla, tedy
Ai = Bj -> Li,j = Li-1,j-1 + 1 Ai <> Bj -> Li,j = max (Li-1,j, Li,j-1)
Nejlepší nalezené řešení je nahoře, nebo vlevo. Tím se tabulka naplní, a my budeme znát nejlepší délku v pravém spodním rohu tabulky
Nyní ale nevíme, kde ta písmena jsou. Je tedy nutné si to ukládat do druhé tabulky (onačit si, kudy jsme na které pole přišli, z leva, ze shora (při zpětném průchodu pouze posun), nebo šikmo (při zpětném průchodu výpis a posun)) a následně zrekonstruovat zpětným průchodem. V přednáškách jsou šipky, ukazující kudy se budeme vracet. Při provádění pravidla 2 si samozřejmě tuto informaci musíme také propagovat, pomatujeme si tedy, odkud jsme na každé pole přišli ( v druhé tabulce si to lze označit třeba 0, 1 pro nahoru a do leva, 2 pro šikmo )
A konečně...
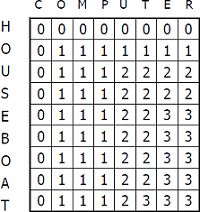
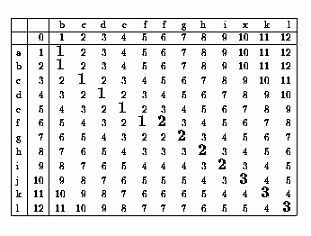
Vzdálenost mezi řetězci
Hammingova metrika: na stejně dlouhé řetězce, jen je porovnáme, a v O(n) čase víme, kolik změn písmen musíme provést (Auto, Zutá = 2)
Levensteinova metrika: někdy také edit distance, máme operace změnit/přidat/odebrat písmeno, abychom dostali z jednoho řetězce ten druhý. Jde o celočíselné vyjádření podobnosti řetězců, například
P=abcdefghijkl, T=bcdeffghixkl, P odpovídá T po 3 změnách (v T přidat a, ubrat f a zaměnit x za j)
Algoritmus: Postup podobný jako u LCS, ale matice je D[i,j] a prvky vyplňujeme takto
máme 3 možné způsoby úpravy řetězce
1. P[i]=T[j] , s = D[i-1,j-1] (shoda) jinak D[i-1,j-1] + 1 (substituce, platíme cenu za změnu znaku)
2. v = D[i-1,j] + 1 (znak navíc v P, neposouváme pointer v T (při úpravách) a platíme cenu za vkládání)
3. r = D[i,j-1] + 1 (znak navíc v T, neposouváme pointer v P (při úpravách) a platíme cenu za rušení)
minimem z s, v a r získáme pole D[i,j]
Řešení je opšt ve spodním pravém rohu a zpět postupujeme po stejných číslech (žádná změna) nebo menších (změna, jdeme-li šikmo, substituce, jdeme-li nahoru rušení, do leva vkládání)